THE APPARENT SPEED PARADOX
The Geometry You Already See
Every rotating object demonstrates a fundamental truth about reality. You've observed it your entire life. Now understand it.
The Observation
Watch a vinyl record spin on a turntable. The outer edge races past you while the center barely moves. Same record. Same rotation. Different speeds.
This isn't complicated physics. It's geometry you can see with your own eyes.

A vinyl record spinning - the outer edge travels faster than the center
The Paradox Named
Every point on a rotating object completes one full rotation in the exact same time. But the outer edge travels a longer distance than the center in that time.
Angular velocity (ω) = constant
Linear velocity (v) = ω × r
∴ Linear velocity increases with radius
This is the Apparent Speed Paradox. Angular velocity remains constant while linear velocity varies with distance from the center.
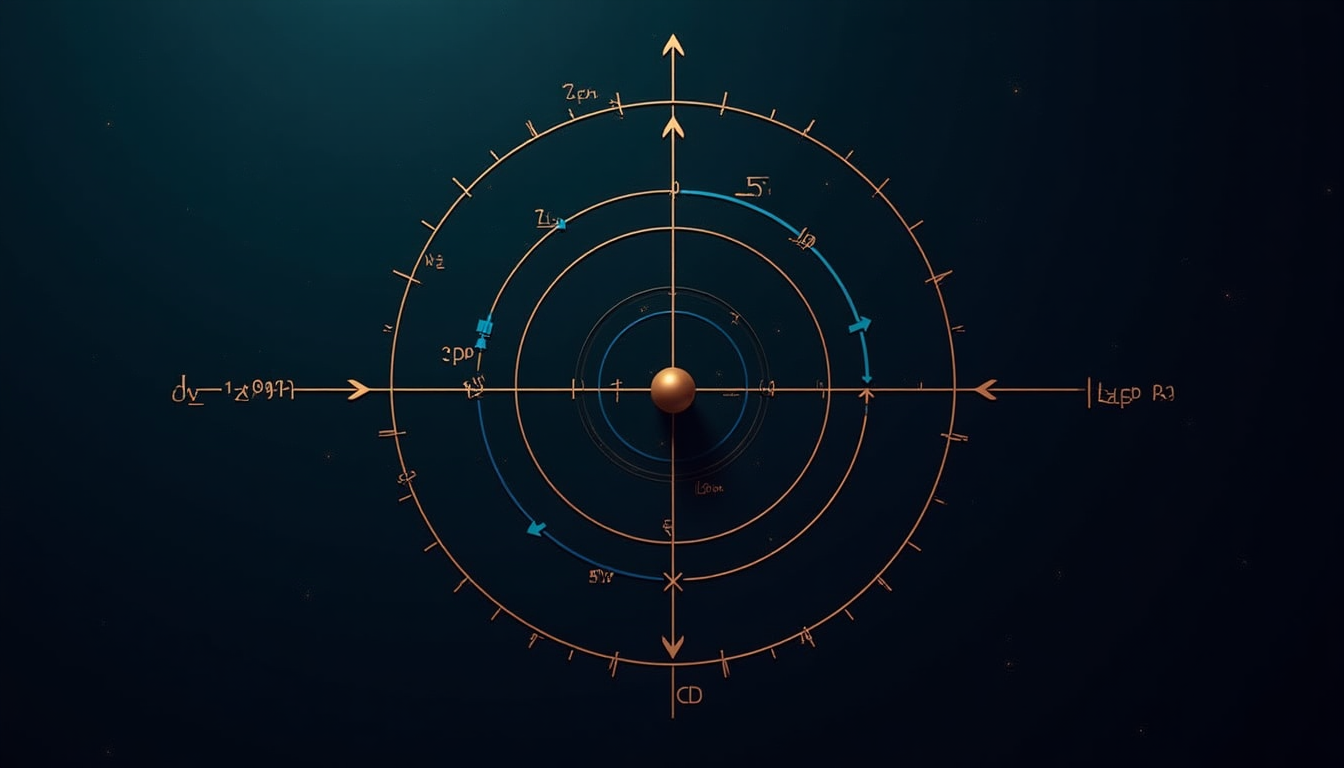
The geometry of rotation - same angular velocity, different linear velocities
Example 1: Gears
Watch two gears mesh together. The small gear spins faster than the large gear. But their teeth meet perfectly at the point of contact.
Why? Because at that exact point, they're moving at identical linear speeds. The geometry forces it.

Meshing gears - different angular velocities, matched linear velocity at contact

A small gear with half the radius must spin twice as fast to match edge speeds
This is why gear ratios work. This is why your car can accelerate. The paradox isn't a problem — it's the solution.
Example 2: Propellers
Look at an airplane propeller. Notice how the blade twists? Near the hub, the blade is angled steeply. Near the tip, it's nearly flat.

A propeller blade - the twist compensates for varying linear velocity

Hub section: steep angle. Tip section: shallow angle.
The tip moves through air much faster than the hub. To generate uniform thrust across the entire blade, engineers must account for the Apparent Speed Paradox. Every propeller you've ever seen is shaped by this principle.
Example 3: Flagella
Now consider something you've never thought about. A single-celled organism swimming through water. Its flagellum — that whip-like tail — rotates like a propeller.
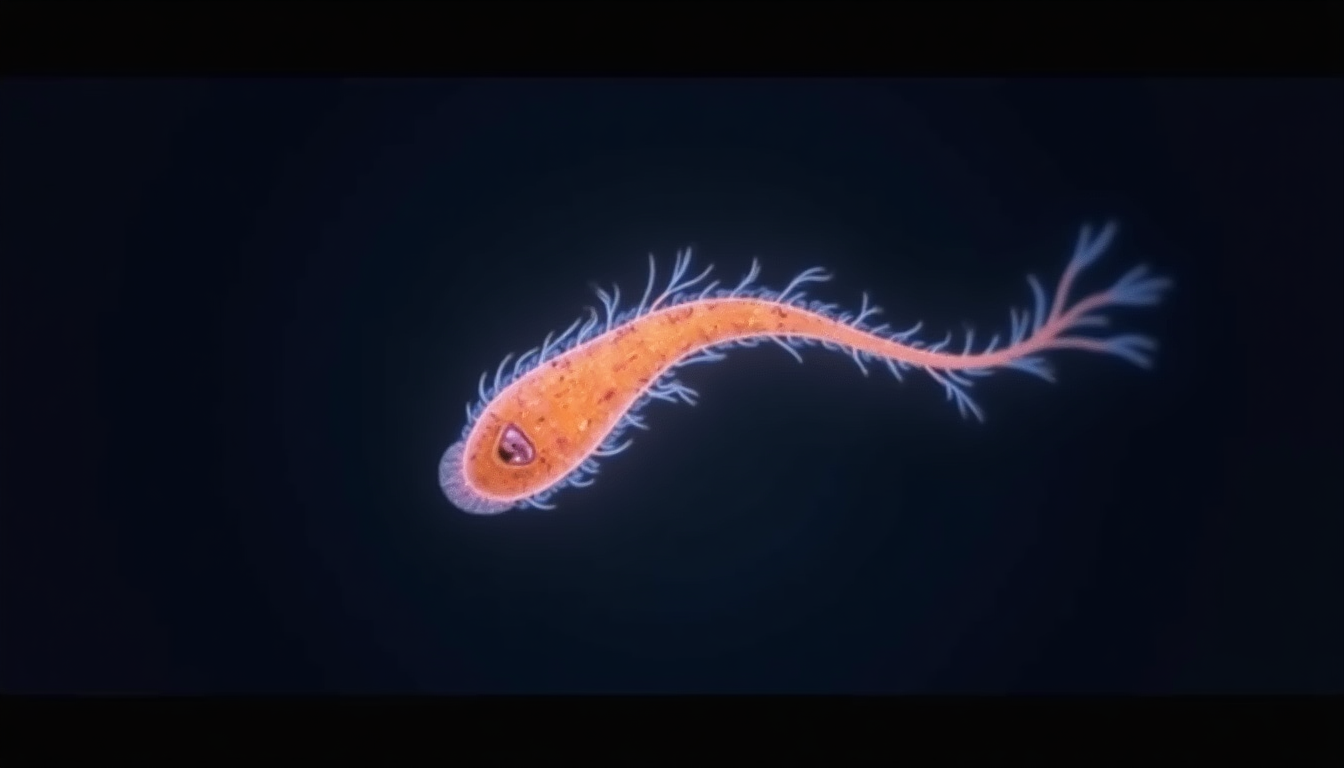
A protozoan's rotating flagellum creates wave motion through differential speeds
The base rotates. The tip follows. But the tip travels a longer path in the same time, creating that characteristic wave motion.
Life itself discovered this geometry billions of years before we named it. The same paradox that spins your records propels the smallest living things.
"The geometry cannot lie."
The Deeper Pattern
Vinyl Records
Groove compression toward center preserves constant playback speed
Gears
Ratio mathematics enabling mechanical advantage
Propellers
Blade twist compensating for radial velocity gradient
Flagella
Wave propagation through differential rotation
Four completely different systems. One geometric principle.
This isn't just interesting trivia. This is a window into how reality structures itself. The same geometry appears everywhere because geometry IS the structure. Not an approximation. Not a model. The actual architecture.
The Invitation
Next time you see a wheel spin, a gear turn, or a propeller blur... remember: you're watching geometry teach itself.
The Apparent Speed Paradox isn't strange. It's fundamental.
And once you see it, you'll see it everywhere.




